Câu hỏi
(B2005) Cho \(A\left( {2;0} \right);\,\,B\left( {6;4} \right).\) Lập phương trình đường tròn (C) tiếp xúc với trục Ox tại A và khoảng cách từ tâm I đến B là 5.
- A \(\left[ \begin{array}{l}{\left( {x - 2} \right)^2} + {\left( {y - 7} \right)^2} = 49\\{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 1\end{array} \right.\)
- B \(\left[ \begin{array}{l}{\left( {x + 2} \right)^2} + {\left( {y - 7} \right)^2} = 49\\{\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 1\end{array} \right.\)
- C \({\left( {x - 2} \right)^2} + {\left( {y + 7} \right)^2} = 49\)
- D \({\left( {x - 2} \right)^2} + {\left( {y + 7} \right)^2} = 1\)
Lời giải chi tiết:
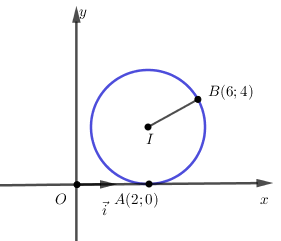
+) Giả sử tâm \(I\left( {a;b} \right)\) ; \(\overrightarrow i \left( {1;0} \right)\)
Ta có: \(\overrightarrow {IA} .\overrightarrow i = 0 \Rightarrow \left( {2 - a} \right).1 = 0 \Leftrightarrow a = 2\) ; Lại có: \(IB = 5 \Leftrightarrow {\left( {6 - 2} \right)^2} + {\left( {b - 4} \right)^2} = {5^2} \Leftrightarrow \left[ \begin{array}{l}b = 7\\b = 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}I\left( {2;7}\right)\\I\left( {2;1} \right)\end{array} \right.\)
Khi đó ta có phương trình đường tròn (C) là: \(\left[ \begin{array}{l}{\left( {x - 2} \right)^2} + {\left( {y - 7} \right)^2} = 49\\{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 1\end{array} \right.\)
Chọn A.







