Lời giải chi tiết:

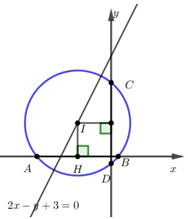
+) Giả sử \(I\left( {a;b} \right),I \in \left( d \right) \Rightarrow 2a - b + 3 = 0\,\,\left( 1 \right)\)

+) Có \(AB = CD \Rightarrow d\left( {I;Ox} \right) = d\left( {I;Oy} \right) \Rightarrow \left| a \right| = \left| b \right| \Rightarrow \left[ \begin{array}{l}a = b\,\,\,\,\,\left( 2 \right)\\a =  - b\,\,\left( {2'} \right)\end{array} \right.\)

+) Giải hệ phương trình gồm có (1) và (2) ta có: \(\left\{ \begin{array}{l}2a - b + 3 = 0\\a = b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 3\\b =  - 3\end{array} \right. \Rightarrow I\left( { - 3; - 3} \right)\)

Có \(IH = d\left( {I;Ox} \right) = 3\)

\(R = IB = \sqrt {I{H^2} + {{\left( {\frac{{AB}}{2}} \right)}^2}}  = \sqrt {9 + 1}  = \sqrt {10} \)  

Khi đó ta có phương trình đường tròn (C) cần tìm là: \({\left( {x + 3} \right)^2} + {\left( {y + 3} \right)^2} = 10.\)

+) Giải hệ phương trình gồm có (1) và (2’) ta có : \(\left\{ \begin{array}{l}2a - b + 3 = 0\\a =  - b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b = 1\end{array} \right. \Rightarrow I\left( { - 1;1} \right)\)

Có \(IH = d\left( {I;Ox} \right) = 1\)

\(R = IB = \sqrt {I{H^2} + {{\left( {\frac{{AB}}{2}} \right)}^2}}  = \sqrt {1 + 1}  = \sqrt 2 \) 

Khi đó ta có phương trình đường tròn (C) cần tìm là: \({\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = 2.\)

Vậy có 2 phương trình đường tròn (C) thỏa mãn: \({\left( {x + 3} \right)^2} + {\left( {y + 3} \right)^2} = 10.\) và \({\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = 2.\)

Chọn A.