Câu hỏi
Cho tam giác ABC. Bên ngoài tam giác ABC vẽ các hình bình hành ABMN, BCEF, CAHK. Chứng minh rằng \(\overrightarrow {FM} + \overrightarrow {NH} + \overrightarrow {KE} = \overrightarrow 0 \)
Lời giải chi tiết:
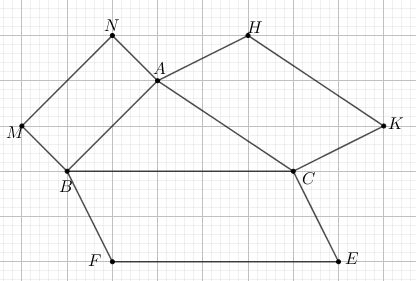
+) Ta có: \(\begin{array}{l}\overrightarrow {FM} = \overrightarrow {FB} + \overrightarrow {BM} \,\,\left( 1 \right)\\\overrightarrow {NH} = \overrightarrow {NA} + \overrightarrow {AH} \,\,\left( 2 \right)\\\overrightarrow {KE} = \overrightarrow {KC} + \overrightarrow {CE} \,\,\left( 3 \right)\end{array}\)
+) Lấy (1) + (2) + (3) ta có:
\(VT = \left( {\overrightarrow {FB} + \overrightarrow {CE} } \right) + \left( {\overrightarrow {BM} + \overrightarrow {NA} } \right) + \left( {\overrightarrow {AH} + \overrightarrow {KC} } \right) = \overrightarrow 0 = VP\)
Ta có điều phải chứng minh.
Câu hỏi trước
