Câu hỏi
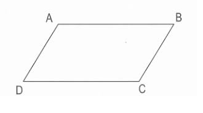
Cho hình bình hành \(ABCD\). Xét các khẳng định sau
\(i)\,\overrightarrow {AB} = \,\overrightarrow {CD} \).
\(ii)\,\overrightarrow {AC} = \,\overrightarrow {BD} \).
\(iii)\,\overrightarrow {AD} = \,\overrightarrow {CB} \).
\(iv)\,\overrightarrow {AC} = \,\overrightarrow {AD} - \,\overrightarrow {BA} \).
Số khẳng định đúng là:
- A 0
- B 1
- C 2
- D 3
Phương pháp giải:
Hai vectơ bằng nhau là hai vectơ cùng hướng và cùng độ dài.
Sử dụng quy tắc hình bình hành \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
Lời giải chi tiết:
Có 1 khẳng định đúng, đó là: iv)
(Do \(\overrightarrow {AC} = \,\overrightarrow {AD} + \,\overrightarrow {AB} = \overrightarrow {AD} - \,\overrightarrow {BA} \) (theo quy tắc hình bình hành)).
Chọn: B
Câu hỏi trước
