Câu hỏi
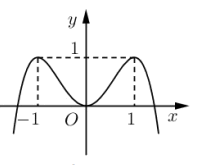
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\left( {a,b,c \in R} \right).\) Đồ thị của hàm số \(y = f\left( x \right)\) như hình vẽ bên. Số nghiệm thực của phương trình \(4f\left( x \right) - 3 = 0\) là:
- A 4
- B 3
- C 2
- D 0
Phương pháp giải:
Ta đưa bài toán về tương giao của 2 đồ thị để làm
Lời giải chi tiết:
\(4f\left( x \right) - 3 = 0 \Leftrightarrow f\left( x \right) = \frac{3}{4}\). Ta thấy: \(CT = 0 < \frac{3}{4} < 1 = CD\)
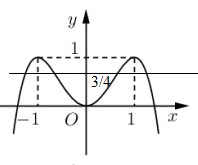
Khi đó số nghiệm thực của phương trình \(4f\left( x \right) - 3 = 0\) chính là số giao điểm của 2 đồ thị \(y = f\left( x \right);y = \frac{3}{4}\)
Nhìn vào đồ thị hàm số ta có 2 đồ thị giao nhau tại 4 điểm phân biệt, nên phương trình đã cho có 4 nghiệm thực.
Chọn A.
Câu hỏi trước
