Phương pháp giải:

- Nhận xét \(\frac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}} = 6\) là hệ số góc của phương trình tiếp tuyến tại \(A\)

- Giải phương trình \(f'\left( x \right) = 6\) tìm nghiệm và thử lại, kiểm tra số giao điểm của tiếp tuyến với đồ thị là \(3\) thì thỏa mãn.

Lời giải chi tiết:

Gọi \(A\left( {{x_0};{y_0}} \right)\), ta có: \({y_1} - {y_2} = 6\left( {{x_1} - {x_2}} \right) \Rightarrow \frac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}} = 6\)  chính là hệ số góc của tiếp tuyến tại \(A\)

Suy ra \(f'\left( {{x_0}} \right) = x_0^3 - 7{x_0} = 6 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 3\\{x_0} =  - 1\\{x_0} =  - 2\end{array} \right.\)

Ta được các tiếp tuyến \(y = 6x - \frac{{117}}{4},y = 6x + \frac{{11}}{4},y = 6x + 2\)

Xét phương trình hoành độ giao điểm của đồ thị hàm số đã cho với đường thẳng \(y = 6x + m\) là

\(\frac{1}{4}{x^4} - \frac{7}{2}{x^2} = 6x + m \Leftrightarrow m = \frac{1}{4}{x^4} - \frac{7}{2}{x^2} - 6x\,\,\,\left( * \right)\)

Xét \(g\left( x \right) = \frac{1}{4}{x^4} - \frac{7}{2}{x^2} - 6x\) có \(g'\left( x \right) = {x^3} - 7x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x =  - 1\\x =  - 2\end{array} \right.\)

Bảng biến thiên:

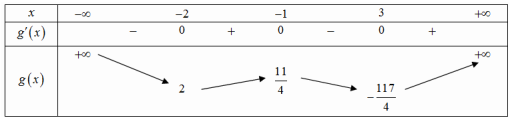
Để phương trình \(\left( * \right)\) có ba nghiệm thì \(m = \frac{{11}}{4}\) và \(m = 2\) ứng với \({x_0} =  - 1\) và \({x_0} =  - 2\)

Vậy có hai điểm \(A\) thỏa mãn yêu cầu đề bài.

Chọn B.