Câu hỏi
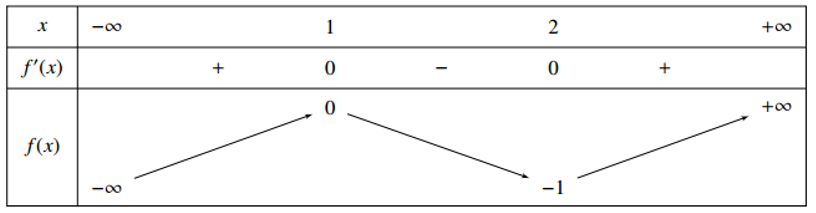
Cho hàm số \(y=f\left( x \right)\) xác định trên R và có bảng biến thiên như sau :
Tìm tất cả các giá trị của tham số m để đồ thị hàm số \(y=|f\left( |x| \right)+m|\) có 11 điểm cực trị
- A \(m\ge 0\)
- B \(m\le 0\)
- C \(0\le m\le 1\)
- D 0 < m < 1
Phương pháp giải:
Cho hàm số \(y=f\left( x \right)\) liên tục trên R . Ta dựng
+)Đồ thị hàm số \(y=f(|x|)\) bằng cách bỏ toàn bộ phần đồ thị \(y=f\left( x \right)\) ở phần bên trái trục tung và lấy đối xứng phần bên phải . Như vậy nếu đồ thị hàm số \(y=f\left( x \right)\) có n điểm cực trị ở phần bên phải trục tung thì đồ thị hàm số \(y=f(|x|)\) sẽ có 2n + 1 điểm cực trị ( do lấy đối xứng + 1 điểm cực trị nằm ở trục tung .
+) Đồ thị hàm số \(y=|f\left( x \right)|\) bằng cách bỏ toàn bộ phần đồ thị \(y=f\left( x \right)\) nằm bên dưới trục hoành , lấy đối xứng phần bỏ đi đó qua trục hoành . Vậy nếu đồ thị hàm số \(y=f\left( x \right)\) có n điểm cực trị thì đồ thị hàm số \(y=|f\left( x \right)|\) sẽ có n + p điểm cực trị với p là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) với trục Ox
Lời giải chi tiết:
Xét đồ thị \(y=|f\left( |x| \right)+m|\) khi m thay đổi thì đồ thị hàm số sẽ tịnh tiến dọc theo trục Oy. Từ bảng biến thiên ta thấy \(y=f\left( x \right)\) đồ thị hàm số đã có 2 điểm cực trị nằm bên phải trục Oy.Vậy nếu giả sử \(y=f\left( x \right)+m\) cắt Ox tại 3 điểm có hoành độ dương thì đồ thị hàm số \(y=|f\left( x \right)+m|\) sẽ có 5 điểm cực trị ( theo lí thuyết phần phương pháp ) , suy ra đồ thị hàm số \(y=|f\left( |x| \right)+m|\) sẽ có 11 điểm cực trị ( theo lí thuyết phần phương pháp ) . Như vậy ta tìm điều kiện của m để phương trình \(f\left( x \right)+m=0\) có 3 nghiệm dương phân biệt. Từ bảng biến thiên dễ thấy với 0 < m < 1 thỏa mãn
Chọn đáp án D