Câu hỏi
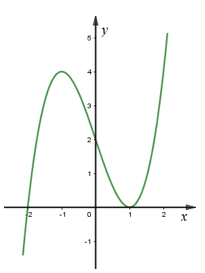
Cho hàm số \(y={{x}^{3}}-3x+2\) có đồ thị như hình vẽ. Giá trị của m để phương trình \(\left| {{x}^{3}}-3x+2 \right|={{2}^{m}}\) có 3 nghiệm thực là
- A \(m=4\).
- B \(0<m<4\).
- C \(m>2\).
- D \(m=2\)
Phương pháp giải:
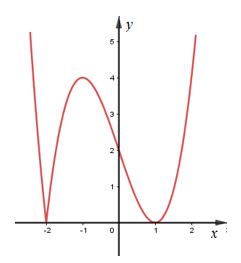
Vẽ đồ thị hàm số \(y=\left| {{x}^{3}}-3x+2 \right|\) dựa vào đồ thị hàm số \(y={{x}^{3}}-3x+2\).
Đánh giá vị trí của đường thẳng \(y={{2}^{m}}\) để đồ thị hàm số cắt đường thẳng \(y={{2}^{m}}\) tại 3 điểm phân biệt.
Kết luận giá trị của m.
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y=\left| {{x}^{3}}-3x+2 \right|\) dựa vào đồ thị hàm số \(y={{x}^{3}}-3x+2\).
Đánh giá vị trí của đường thẳng \(y={{2}^{m}}\) để đồ thị hàm số cắt đường thẳng \(y={{2}^{m}}\) tại 3 điểm phân biệt.
Kết luận giá trị của m.
Câu hỏi trước
