Phương pháp giải:

Sử dụng phương pháp hàm số.

Lời giải chi tiết:

\(2{{x}^{3}}-3{{x}^{2}}+2-{{2}^{1-2m}}=0\Leftrightarrow 2{{x}^{3}}-3{{x}^{2}}+2={{2}^{1-2m}}\)

Xét hàm số \(f\left( x \right)=2{{x}^{3}}-3{{x}^{2}}+2\)

 TXĐ: \(D=R\)  Có  \(y' = 6{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 1
\end{array} \right.\)

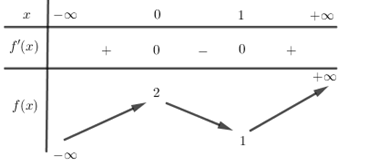
Lập BBT:

Số nghiệm của phương trình \(2{{x}^{3}}-3{{x}^{2}}+2={{2}^{1-2m}}\) là số giao điểm của đồ thị hàm số \(f\left( x \right)=2{{x}^{3}}-3{{x}^{2}}+2\) và đường thẳng \(y={{2}^{1-2m}}\).

Dựa vào BBT, phương trình có 3 nghiệm phân biệt \(\Rightarrow 1<{{2}^{1-2m}}<2\Leftrightarrow 0<1-2m<1\Leftrightarrow 0<m<\frac{1}{2}\)

Chọn B.