Câu hỏi
Cho hàm số \(y={{x}^{3}}+b{{x}^{2}}-x+d\)
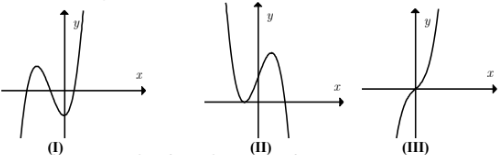
Các đồ thị nào có thể là đồ thị biểu diễn hàm số đã cho?
- A (I)
- B (I) và (II)
- C (III)
- D (I) và (III)
Phương pháp giải:
Dựa vào hình dáng của đồ thị hàm số để chọn đáp án đúng.
Lời giải chi tiết:
Ta có: \(y'=3{{x}^{2}}+2bx-1\Rightarrow y'=3{{x}^{2}}+2bx-1=0\)
Có \(\Delta ={{b}^{2}}+3>0\Rightarrow pt\ y'=0\) có hai nghiệm phân biệt hay đồ thị hàm số có hai điểm cực trị.
\(\Rightarrow \) hình (III) không đúng.
Gọi \({{x}_{1}}<{{x}_{2}}\) là hai nghiệm của phương trình \(y'=0\) Ta có:
Khi đó hàm số đồng biến trên \(\left( -\infty ;\ {{x}_{1}} \right)\) và \(\left( {{x}_{2}};+\infty \right)\) .
Hàm số nghịch biến trên \(\left( {{x}_{1}};\ {{x}_{2}} \right)\)
\(\Rightarrow \) chỉ có hình (I) thỏa mãn.
Chọn A.