Câu hỏi
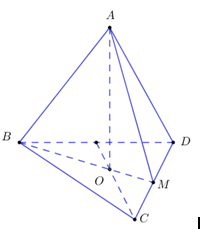
Cho tứ diện đều ABCD có cạnh bằng 3a. Hình nón (N) có đỉnh A, đáy là đường tròn ngoại tiếp tam giác BCD. Tính theo a diện tích xung quanh \({{S}_{xq}}\) của (N).
- A \({{S}_{xq}}=3\sqrt{3}\pi {{a}^{2}}\)
- B \({{S}_{xq}}=6\pi {{a}^{2}}\)
- C \({{S}_{xq}}=6\sqrt{3}\pi {{a}^{2}}\)
- D \({{S}_{xq}}=12\pi {{a}^{2}}\)
Phương pháp giải:
Công thức tính diện tích xung quanh của hình nó có bán kính đáy \(R\) và đường sinh \(l\) là: \({{S}_{xq}}=\pi Rl\)
Lời giải chi tiết:
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(BCD\)
Khi đó: \(BM = \frac{{3a\sqrt 3 }}{2} \Rightarrow BO = R = \frac{2}{3}.\frac{{3a\sqrt 3 }}{2} = a\sqrt 3 .\)
\(\Rightarrow {{S}_{xq\ \left( N \right)}}=\pi Rl=\pi .a\sqrt{3}.3a=3\sqrt{3}\pi {{a}^{2}}\)
Chọn A.
Câu hỏi trước
