Câu hỏi
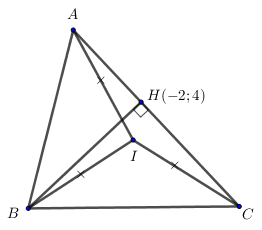
(D2013) Cho tam giác ABC có \(M\left( { - \frac{9}{2};\frac{3}{2}} \right)\) là trung điểm của AB. \(H\left( { - 2;4} \right)\) và \(I\left( { - 1;1} \right)\) lần lượt là chân đường cao kẻ từ B và tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ điểm C.
- A C(4;-1); hoặc C(1;6)
- B C(4;1); hoặc C(-1;6)
- C C(-4;-1); hoặc C(1;6)
- D C(-4;1); hoặc C(1;-6)
Lời giải chi tiết:
Giả sử \(A\left( {a;b} \right)\). M là trung điểm của AB \( \Rightarrow B\left( { - 9 - a;3 - b} \right)\)
\(I{A^2} = I{B^2} \Leftrightarrow {\left( { - 1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( { - 8 - a} \right)^2} + {\left( {2 - b} \right)^2}\,\,\,\left( 1 \right)\)
\(\begin{array}{l}\left\{ \begin{array}{l}\overrightarrow {HA} = \left( {a + 2;b - 4} \right)\\\overrightarrow {HB} = \left( { - 7 - a; - 1 - b} \right)\end{array} \right.\\\overrightarrow {HA} .\overrightarrow {HB} = 0 \Leftrightarrow \left( {a + 2} \right)\left( { - 7 - a} \right) + \left( {b - 4} \right)\left( { - 1 - b} \right) = 0\,\,\,\left( 2 \right)\end{array}\)
Giải hệ \[\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}A\left( { - 4;5} \right);B\left( { - 5; - 2} \right)\\A\left( { - 5; - 2} \right);B\left( { - 4;5} \right)\end{array} \right.\]
TH1 : \(A\left( { - 4;5} \right);B\left( { - 5; - 2} \right).\) Giả sử \(C\left( {m;n} \right)\)
\(\left\{ \begin{array}{l}\overrightarrow {AH} //\overrightarrow {AC} \\IA = IC\end{array} \right. \Rightarrow C\left( {4;1} \right)\)
TH2 : \(A\left( { - 5; - 2} \right);B\left( { - 4;5} \right)\). Giả sử \(C\left( {c;d} \right)\).
\(\left\{ \begin{array}{l}\overrightarrow {AH} //\overrightarrow {AC} \\IA = IC\end{array} \right. \Rightarrow C\left( { - 1;6} \right)\)







