Lời giải chi tiết:

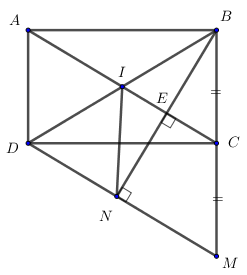
Giả sử \(C\left( {a;b} \right)\)

\(C \in \left( d \right):\,\,2a + b + 5 = 0\,\,\,\left( 1 \right)\)

I là trung điểm của AC \( \Rightarrow I\left( {\frac{{a - 4}}{2};\frac{{b + 8}}{2}} \right)\)

\({\Delta _v}BND\) có NI là trung tuyến \( \Rightarrow NI = \frac{{BD}}{2} = IA \Rightarrow I{A^2} = I{N^2}\)

\( \Rightarrow {\left( {\frac{{a - 4}}{2} + 4} \right)^2} + {\left( {\frac{{b + 8}}{2} - 8} \right)^2} = {\left( {\frac{{a - 4}}{2} - 5} \right)^2} + {\left( {\frac{{b + 8}}{2} + 4} \right)^2}\,\,\,\left( 2 \right)\)

Giải hệ \(\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow C\left( {1; - 7} \right)\)

* Tìm B.

\(\left\{ \begin{array}{l}CM//AD\\CM = AD\end{array} \right. \Rightarrow \) Tứ giác ACMD là hình bình hành.

\( \Rightarrow CA//DM \Rightarrow CE//MN \Rightarrow CE\) là đường trung bình của tam giác BMN.

\( \Rightarrow B\) đối xứng với N qua AC.

Giả sử \(B\left( {c;d} \right) \Rightarrow E\left( {\frac{{c + 5}}{2}'\frac{{d - 4}}{2}} \right)\)

\(\left\{ \begin{array}{l}\overrightarrow {AE} //\overrightarrow {AC} \\\overrightarrow {BN} .\overrightarrow {AC}  = 0\end{array} \right. \Rightarrow B\left( { - 4; - 7} \right)\).