Lời giải chi tiết:

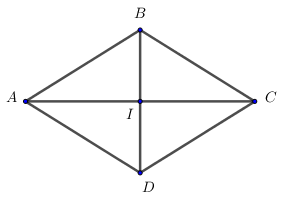
a) Tìm B.

Giả sử \(B\left( {m;n} \right) \Rightarrow I\left( {\frac{{m + 1}}{2};\frac{{n - 3}}{2}} \right) \in AC\)

\(\begin{array}{l} \Rightarrow \frac{{2\left( {m + 1} \right)}}{2} + \frac{{n - 3}}{2} - 4 = 0\\ \Leftrightarrow 2m + n - 9 = 0\,\,\left( 1 \right)\end{array}\)

\(\begin{array}{l}\left\{ \begin{array}{l}\overrightarrow {DB}  = \left( {m - 1;n + 3} \right)\\{\overrightarrow u _{AC}} = \left( {1; - 2} \right)\end{array} \right.\\\overrightarrow {DB} .{\overrightarrow u _{AC}} = 0 \Leftrightarrow  - m + 2n + 7 = 0\,\,\left( 2 \right)\end{array}\)

Giải hệ \(\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow B\left( {5; - 1} \right) \Rightarrow I\left( {3; - 2} \right) \Rightarrow IB = \sqrt 5 \)

b) Tìm A, C.

Giả sử \(A\left( {a;b} \right).\) I là trung điểm của AC \( \Rightarrow C\left( {6 - a; - 4 - b} \right)\).

\(\begin{array}{l}A \in AC \Rightarrow 2a + b - 4 = 0\,\,\,\left( 3 \right)\\{S_{\Delta IAB}} = \frac{{20}}{4} = 5 = \frac{1}{2}IA.IB = \frac{1}{2}IA.\sqrt 5 \\ \Rightarrow IA = 2\sqrt 5  \Leftrightarrow {\left( {a - 3} \right)^2} + {\left( {b + 2} \right)^2} = 20\,\,\left( 4 \right)\end{array}\)

Giải hệ \(\left\{ \begin{array}{l}\left( 3 \right)\\\left( 4 \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}A\left( {1;2} \right)\,\,\left( {ktm} \right)\\A\left( {5; - 6} \right)\,\,\left( {tm} \right) \Rightarrow C\left( {1;2} \right)\end{array} \right.\).