Câu hỏi
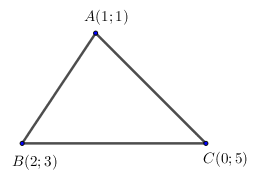
\(\Delta ABC;\,\,A\left( {1;1} \right);\,\,B\left( {2;3} \right);\,\,C\left( {0;5} \right).\,\,\Delta ABC\) nhọn hay vuông hay tù?
- A Tam giác ABC nhọn
- B Tam giác ABC vuông tại A
- C Tam giác ABC tù ở B
- D Tam giác ABC tù ở C.
Lời giải chi tiết:
\(\left\{ \begin{array}{l}\overrightarrow {AB} = \left( {1;2} \right)\\\overrightarrow {AC} = \left( { - 1;4} \right)\end{array} \right.;\,\,\cos \widehat A = \cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{ - 1 + 8}}{{AB.AC}} > 0 \Rightarrow \widehat A\) nhọn.
\(\left\{ \begin{array}{l}\overrightarrow {BA} = \left( { - 1; - 2} \right)\\\overrightarrow {BC} = \left( { - 2;2} \right)\end{array} \right..\,\,\cos \widehat B = \cos \left( {\overrightarrow {BA} ;\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{2 - 4}}{{BA.BC}} < 0 \Rightarrow \widehat B\) tù.
\( \Rightarrow \Delta ABC\) tù ở B.
Chọn C.







