Câu hỏi
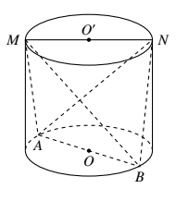
Cho hình trụ có đường cao h, các đường tròn đáy lần lượt là \(\left( {O;R} \right)\) và \(\left( {O';R} \right)\). AB là đường kính cố định của \(\left( {O;R} \right)\) và MN là một đường kính thay đổi trên \(\left( {O';R} \right)\). Tính giá trị lướn nhất của thể tích khối tứ diện MNAB.
- A \({V_{\max }} = \frac{{2{R^2}h}}{3}\)
- B \({V_{\max }} = \frac{{{R^2}h}}{3}\)
- C \({V_{\max }} = 2{R^2}h\)
- D \({V_{\max }} = \frac{{{R^2}h}}{6}\)
Phương pháp giải:
Sử dụng công thức tính thể tích \({V_{ABCD}} = \frac{1}{6}AB.CD.d\left( {AB;CD} \right).\sin \widehat {\left( {AB;CD} \right)}\).
Lời giải chi tiết:
Ta có \(AB = MN = 2R;\,\,d\left( {AB;CD} \right) = {d_{\left( {2\,day} \right)}} = h\)
\( \Rightarrow {V_{MNAB}} = \frac{1}{6}.AB.MN.d\left( {AB;MN} \right).\sin \widehat {\left( {AB;MN} \right)} = \frac{1}{6}.4{R^2}h.\sin \widehat {\left( {AB;MN} \right)} = \frac{{2{R^2}h}}{3}\sin \widehat {\left( {AB;MN} \right)}\)
Để \({V_{MNAB\,\,\max }} \Leftrightarrow \sin {\widehat {\left( {AB;MN} \right)}_{\max }} \Rightarrow \sin \widehat {\left( {AB;MN} \right)} = 1 \Leftrightarrow AB \bot MN\).
Vậy \({V_{\max }} = \frac{{2{R^2}h}}{3}\).
Chọn A.