Câu hỏi
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy góc \({60^0}\). Hình nón có đỉnh S, đáy là đường tròn nội tiếp tứ giác ABCD có diện tích xung quanh là:
- A \(S = \frac{3}{2}\pi {a^2}\).
- B \(S = \pi {a^2}\).
- C \(S = \frac{{\pi {a^2}\left( {\sqrt 7 + 1} \right)}}{4}\).
- D \(S = \frac{{\pi {a^2}\sqrt 7 }}{4}\).
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi Rl\)
Lời giải chi tiết:
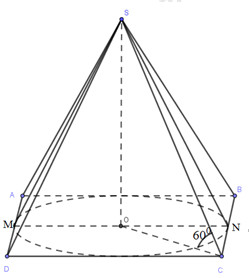
ABCD là hình vuông có O là tâm \( \Rightarrow OC = \frac{{AB}}{{\sqrt 2 }} = \frac{a}{{\sqrt 2 }},\,\,\,ON = \frac{{AB}}{2} = \frac{a}{2}\)
\(\Delta SOC\) vuông tại O , \(\widehat {SCO} = {60^0} \Rightarrow SO = OC.\tan {60^0} = \frac{a}{{\sqrt 2 }}.\sqrt 3 = a\sqrt {\frac{3}{2}} \)
\(\Delta SON\) vuông tại O\( \Rightarrow SN = \sqrt {S{O^2} + O{N^2}} = \sqrt {\frac{3}{2}{a^2} + \frac{1}{4}{a^2}} = \frac{{\sqrt 7 }}{2}a\)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi Rl = \pi .\frac{a}{2}.a\frac{{\sqrt 7 }}{2} = \frac{{\pi \sqrt 7 {a^2}}}{4}\)
Chọn: D







