Câu hỏi
Đường cong ở hình bên là đồ thị của một trong các hàm số sau, hỏi đó là hàm số nào?
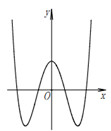
- A \(y = {x^4} + 3{x^2} + 1\).
- B \(y = {x^4} - 3{x^2} + 1\).
- C \(y = - {x^4} + 3{x^2} + 1\).
- D \(y = {x^3} - 3{x^2} + 1\).
Phương pháp giải:
Nhận biết dạng đồ thị của hàm số bậc 4 trùng phương và hàm số bậc ba.
Lời giải chi tiết:
Quan sát đồ thị, ta thấy :
+ Đồ thị hàm số không phải đồ thị của hàm số bậc ba \( \Rightarrow \) Loại phương án D
\( \Rightarrow \)Xét các hàm số bậc bốn trùng phương:
+ Nét cuối cùng của đồ thị hàm số đi lên \( \Rightarrow \)\(a > 0 \Rightarrow \)Loại phương án C
+ Đồ thị hàm số có 3 điểm cực trị \( \Rightarrow \) Loại phương án A, vì:
\(y = {x^4} + 3{x^2} + 1 \Rightarrow y' = 4{x^3} + 6x,\,\,\,y' = 0\) có 1 nghiệm duy nhất.
Và \(y = {x^4} - 3{x^2} + 1 \Rightarrow y' = 4{x^3} - 6x,\,\,\,y' = 0\) có 3 nghiệm phân biệt \( \Rightarrow \) Chọn B
Chọn: B







