Câu hỏi
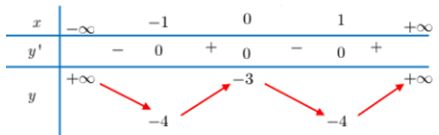
Bảng biến thiên sau là của hàm số nào dưới đây?
- A \(y=\frac{1}{2}{{x}^{4}}-{{x}^{2}}-3\)
- B \(y=2{{x}^{4}}-4{{x}^{2}}-3\)
- C \(y=2{{\left| x \right|}^{3}}-3\left| x \right|-3\)
- D \(y=2\left| {{x}^{3}} \right|-3{{x}^{2}}-3\)
Phương pháp giải:
+) Dựa vào bảng biến thiên, thay các điểm thuộc đồ thị hàm số vào các hàm số ở các đáp án để loại dần các đáp án.
Lời giải chi tiết:
Dựa vào BBT ta thấy hàm số cần tìm có đồ thị đi qua các điểm \(\left( -1;\ -4 \right),\ \left( 0;-3 \right),\ \ \left( 1;-4 \right)\)
Thay tọa độ điểm \(\left( -1;-4 \right)\) vào công thức các hàm số ta loại trừ được đáp án A và B.
+) Đáp án C: Ta có: \(y=2{{\left| x \right|}^{3}}-3\left| x \right|-3=\left\{ \begin{align} & 2{{x}^{3}}-3x-3\ \ \ khi\ \ x\ge 0 \\ & -2{{x}^{3}}+3x-3\ \ \ khi\ \ \ x<0 \\\end{align} \right.\)
Xét hàm số: \(y=2{{x}^{3}}-3x-3\) có \(y'=6{{x}^{2}}-3\Rightarrow y'=0\Leftrightarrow 6{{x}^{2}}-3=0\Leftrightarrow x=\pm \frac{\sqrt{2}}{2}\Rightarrow x=\frac{\sqrt{2}}{2}\ \ \left( do\ \ x\ge 0 \right)\)
\(\Rightarrow \) hàm số có một điểm cực trị \(x=\frac{\sqrt{2}}{2}\) mà trên BBT, hàm số chỉ có 3 điểm cực trị \(x=-1,\ x=0,\ x=1\Rightarrow \) loại đáp án C.
Chọn D.