Câu hỏi
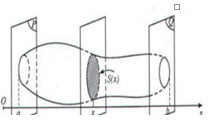
Trong không gian Oxyz, cho vật thể được giới hạn bởi 2 mặt phẳng \((P),\,\,(Q)\) vuông góc với Ox lần lượt tại \(x = a,\,\,x = b,\,\,(a < b)\). Một mặt phẳng tùy ý vuông góc với Ox tại điểm có hoành độ x, \((a \le x \le b)\) cắt vật thể theo thiết diện có diện tích là \(S(x)\), vứi \(y = S(x)\) là hàm số liên tục trên \(\left[ {a;b} \right]\). Thể tích V của vật thế đó được tính theo công thức:
- A \(V = \int\limits_a^b {{S^2}(x)dx} \).
- B \(V = \pi \int\limits_a^b {{S^2}(x)dx} \).
- C \(V = \pi \int\limits_a^b {S(x)dx} \).
- D \(V = \int\limits_a^b {S(x)dx} \).
Lời giải chi tiết:
Thể tích V của vật thế đó được tính theo công thức: \(V = \int\limits_a^b {S(x)dx} \).
Chọn: D
Câu hỏi trước
