Câu hỏi
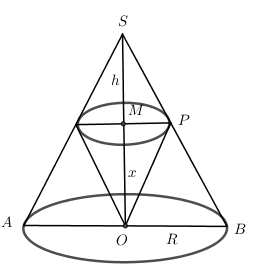
Cho hình nón (N) có đỉnh S, tâm đáy là O. Bán kính đáy bằng R, chiều cao SO = h không đổi. M thuộc SO sao cho OM = x (0 < x < h). Xét nón (N’) đỉnh O, tâm đáy là M. Tìm x để thể tích khối nón (N’) lớn nhất.
- A \(\frac{h}{6}\)
- B \(\frac{h}{4}\)
- C \(\frac{h}{2}\)
- D
\(\frac{h}{3}\)
Lời giải chi tiết:
Nón (N’) có bán kính đáy là R’
+) Ta có: \(\frac{R'}{R}=\frac{SM}{SO}=\frac{h-x}{h}\Rightarrow R'=\frac{\left( h-x \right)R}{h}\)
+) \({{V}_{\left( N' \right)}}=\frac{1}{3}\pi {{\left[ \frac{\left( h-x \right)R}{h} \right]}^{2}}.x=\frac{\pi {{R}^{2}}}{3{{h}^{2}}}{{\left( h-x \right)}^{2}}x.\)
+) Xét \(f\left( x \right)=x{{\left( h-x \right)}^{2}}={{x}^{3}}-2h{{x}^{2}}+{{h}^{2}}x\)
\(\Rightarrow f'\left( x \right)=3{{x}^{2}}-4hx+{{h}^{2}}\Rightarrow f'\left( x \right)=0\Leftrightarrow \left[ \begin{align} & x=h \\ & x=\frac{h}{3} \\ \end{align} \right.\)
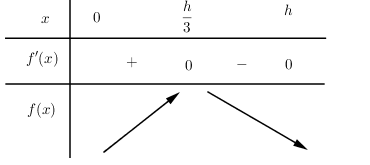
+) Bảng biến thiên:
\(\Rightarrow f\left( x \right)\,\max \Leftrightarrow x=\frac{h}{3}\)
Chọn đáp án D
Câu hỏi trước
