Câu hỏi
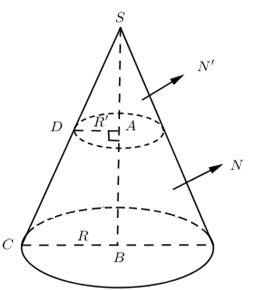
Hình thang ABCD vuông ở A và B. AB = h, AD = R’, BC = R (R > R’). Quay hình thang ABCD một vòng quanh AB. Xây dựng công thức tính thể tích nón cụt tạo thành.
Lời giải chi tiết:
\(+)\,V={{V}_{\left( N \right)}}-{{V}_{\left( N' \right)}}=\frac{1}{3}\pi {{R}^{2}}SB-\frac{1}{3}\pi R{{'}^{2}}SA\,\left( * \right)\)
+) Ta có:
\(\begin{align} & \frac{SA}{SB}=\frac{R'}{R}\Rightarrow \frac{SA}{SB-SA}=\frac{R'}{R-R'} \\ & \Rightarrow SA=\frac{hR'}{R-R'}\Rightarrow SB=SA+h=\frac{hR}{R-R'} \\ \end{align}\)
+) Thay SA, SB vào phương trình (*) ta có:
\(\begin{align} & V=\frac{1}{3}\pi {{R}^{2}}SB-\frac{1}{3}\pi R{{'}^{2}}SA\, \\ & \Leftrightarrow V=\frac{1}{3}\pi {{R}^{2}}.\frac{hR}{R-R'}-\frac{1}{3}\pi R{{'}^{2}}.\frac{hR'}{R-R'} \\ & \Leftrightarrow V=\frac{\pi h\left( {{R}^{3}}-R{{'}^{3}} \right)}{3\left( R-R' \right)}=\frac{\pi h}{3}\left( {{R}^{2}}+R{{'}^{2}}+RR' \right) \\ \end{align}\)