Câu hỏi
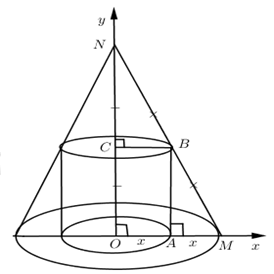
Cho \(\widehat{xOy}\) vuông ở O. Hai điểm M, N di động trên Ox, Oy sao cho MN = 2a không đổi. A, B, C lần lượt là trung điểm của OM, MN, ON. Đặt OA = x \(\left( 0<x<2a \right).\) Quay hình chữ nhật ABCO một vòng quanh CO tạo ra hình trụ có diện tích toàn phần là S2. Quay tam giác vuông NOM một còng quanh ON tạo ra hình nón có diện tích xung quanh là S1. Tính OM để tỉ số \(\frac{{{S}_{2}}}{{{S}_{1}}}\) là lớn nhất.
- A \(\frac{a}{3}\)
- B \(\frac{a}{4}\)
- C \(a\sqrt{2}\)
- D \(a\sqrt{3}\)
Lời giải chi tiết:
+) Trong D vuông BAM có:
\(AB=\sqrt{B{{M}^{2}}-A{{M}^{2}}}=\sqrt{{{a}^{2}}-{{x}^{2}}}=OC\)
+) Diện tích toàn phần trụ là: \({{S}_{2}}=2\pi x.\sqrt{{{a}^{2}}-{{x}^{2}}}+2\pi {{x}^{2}}\)
+) Diện tích xung quanh hình nón là:
\({{S}_{1}}=\pi .OM.MN=\pi .2x.2a=4x\pi a\)
+) \(\Rightarrow \frac{{{S}_{2}}}{{{S}_{1}}}=\frac{2\pi x.\sqrt{{{a}^{2}}-{{x}^{2}}}+2\pi {{x}^{2}}}{4x\pi a}=\frac{x+\sqrt{{{a}^{2}}-{{x}^{2}}}}{2a}\)
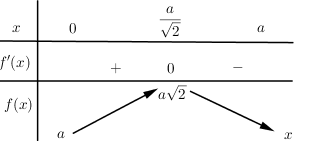
+) Xét \(f\left( x \right)=x+\sqrt{{{a}^{2}}-{{x}^{2}}}\)
\(\begin{align} & \Rightarrow f'\left( x \right)=\frac{\sqrt{{{a}^{2}}-{{x}^{2}}}-x}{\sqrt{{{a}^{2}}-{{x}^{2}}}} \\ & \Rightarrow f'\left( x \right)=0\Leftrightarrow \sqrt{{{a}^{2}}-{{x}^{2}}}-x=0\Leftrightarrow x=\sqrt{{{a}^{2}}-{{x}^{2}}}\Leftrightarrow x=\frac{a}{\sqrt{2}} \\\end{align}\)
Bảng biến thiên:
Để tỉ số \(\frac{{{S}_{2}}}{{{S}_{1}}}\max \Leftrightarrow f\left( x \right)max\Leftrightarrow x=\frac{a}{\sqrt{2}}\Rightarrow OM=2.\frac{a}{\sqrt{2}}=a\sqrt{2}\)
Chọn đáp án C