Câu hỏi
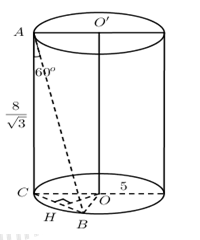
Cho hình trụ có \(R = 5\), \(h=\dfrac{8}{\sqrt{3}}.\) \(OO’\) là trục của hình trụ. \(A,\, B\) thuộc hai đáy trụ sao cho \(\widehat{\left( AB;OO' \right)}={{60}^{0}}\). Tính khoảng cách từ đường thẳng \(AB\) đến đường thẳng \(OO’\).
- A \(2\)
- B \(3\)
- C \(4\)
- D \(5\)
Lời giải chi tiết:
* Ta có: \(\widehat{\left( AB;OO' \right)}=\widehat{\left( AB;AC \right)}=\widehat{CAB}={{60}^{0}}\).
* Tam giác vuông \(ACB\): \(\tan {{60}^{0}}=\dfrac{BC}{AC}\Rightarrow BC=\tan {{60}^{0}}.AC=\sqrt{3}.\dfrac{8}{\sqrt{3}}=8\).
* \((ABC)\) chứa \(AB\) và song song với \(OO’\).
\(\Rightarrow d\left( OO';AB \right)=d\left( O;\left( ABC \right) \right)=OH\).
* \(HB=\dfrac{BC}{2}=4\)
* \({{\Delta }_{v}}OHB:\,\,OH=\sqrt{O{{B}^{2}}-H{{B}^{2}}}=\sqrt{{{5}^{2}}-{{4}^{2}}}=\sqrt{9}=3\)
Chọn đáp án B.
Câu hỏi trước
