Câu hỏi
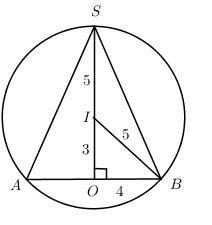
Cho hình nón có đường cao bằng \(8\) nội tiếp trong cầu có bán kính \(R\) bằng \(5\). Tính tỉ số thể tích giữa nón và cầu.
- A \(\dfrac{37}{125}\)
- B \(\dfrac{34}{125}\)
- C \(\dfrac{33}{125}\)
- D \(\dfrac{32}{125}\)
Lời giải chi tiết:
+) \(\Delta\) vuông \(IOB\). Rnón \(=OB=\sqrt{I{{B}^{2}}-I{{O}^{2}}}=\sqrt{{{5}^{2}}-{{3}^{2}}}=4\)
+) Vcầu \(=\dfrac{4}{3}\pi {{R}^{3}}=\dfrac{500\pi }{3}\)
+) Vnón \(=\dfrac{1}{3}\pi {{R}^{2}}h=\dfrac{1}{3}\pi {{.4}^{2}}.8=\dfrac{1}{3}.\pi .16.8=\dfrac{128\pi }{3}\).
+) \(\dfrac{{{V}_{non}}}{{{V}_{cau}}}=\dfrac{\dfrac{128\pi }{3}}{\dfrac{500\pi }{3}}=\dfrac{128}{500}=\dfrac{32}{125}\).
Chọn đáp án D.
Câu hỏi trước
