Câu hỏi
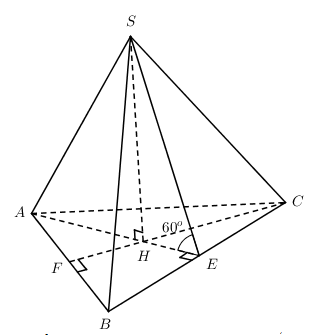
Chóp đều \(S.ABC\), có \(AB = a\). Góc giữa mặt bên và mặt đáy bằng \({{60}^{0}}\). Tính thể tích khối nón nội tiếp trong chóp \(S.ABC\).
- A \(\dfrac{\pi {{a}^{3}}}{36}\)
- B \(\dfrac{\pi {{a}^{3}}}{32}\)
- C \(\dfrac{\pi {{a}^{3}}}{72}\)
- D \(\dfrac{\pi {{a}^{3}}}{64}\)
Lời giải chi tiết:
\(\begin{align}& *\,\,R=HE=\frac{1}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6} \\ & *\,\,\Delta SHE:\,\,\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}={{60}^{0}}=\widehat{SEH} \\ & \tan \,{{60}^{0}}=\dfrac{SH}{HE}\Rightarrow SH=\tan {{60}^{0}}.HE=\sqrt{3}.\dfrac{a\sqrt{3}}{6}=\dfrac{a}{2} \\\end{align}\)
- Thể tích khối nón nội tiếp trong chóp \(S.ABC\): \({{V}_{N}}=\dfrac{1}{3}\pi {{R}^{2}}h=\dfrac{1}{3}\pi {{R}^{2}}.SH=\dfrac{\pi }{3}.{{\left( \dfrac{a\sqrt{3}}{6} \right)}^{2}}.\dfrac{a}{2}=\dfrac{\pi {{a}^{3}}}{72}\).
Chọn đáp án C.
Câu hỏi trước
