Câu hỏi
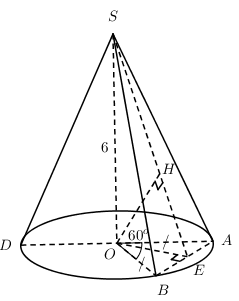
Cho hình nón có bán kính đáy \(R = 2\), chiều cao \(h = 6\), đỉnh \(S\). Vẽ hai đường sinh \(SA,\, SB\) để \(AB\) chắn trên đường tròn đáy vào cung có số đo \({{60}^{0}}\). \(O\) là tâm đường tròn đáy. Tính khoảng cách từ \(O\) xuống mặt phẳng \((SAB)\).
- A \(\dfrac{5}{\sqrt{13}}\)
- B \(\dfrac{6}{\sqrt{13}}\)
- C \(\dfrac{7}{\sqrt{13}}\)
- D \(\dfrac{8}{\sqrt{13}}\)
Lời giải chi tiết:
+) Số đo \(\overset\frown{AB}={{60}^{0}}\Rightarrow \widehat{AOB}={{60}^{0}}\Rightarrow \Delta AOB\,\) đều có cạnh \(2\).
+) Vẽ \(OE\bot BA,\,OH\bot SE\Rightarrow d\left( O;\,\left( SAB \right) \right)=OH\).
+) Ta có: \(OE=\dfrac{2\sqrt{3}}{2}=\sqrt{3};\,\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{E}^{2}}}+\dfrac{1}{S{{O}^{2}}}\Rightarrow OH=\dfrac{6}{\sqrt{13}}\)
Chọn đáp án B.
Câu hỏi trước
