Câu hỏi
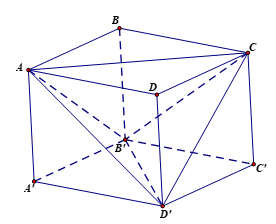
Một hình hộp chữ nhật \(ABCD.{A}'{B}'{C}'{D}'\) có ba kích thước là \(2\operatorname{cm}\), \(3\operatorname{cm}\) và \(6\operatorname{cm}\). Thể tích của khối tứ diện \(AC{B}'{D}'\) bằng
- A
\(12{{\operatorname{cm}}^{3}}\).
- B
\(8{{\operatorname{cm}}^{3}}\).
- C \(6{{\operatorname{cm}}^{3}}\).
- D \(4{{\operatorname{cm}}^{3}}\).
Phương pháp giải:
Tính thể tích khối hộp và dựa vào tỉ số thể tích tìm thể tích khối cần tìm
Lời giải chi tiết:
Hình vẽ tham khảo
Thể tích khối hộp chữ nhật \(ABCD.{A}'{B}'{C}'{D}'\) là \(V=2.3.6=36\,\,\,\left( {{\operatorname{cm}}^{3}} \right)\).
Ta có \({{V}_{A.{A}'{B}'{D}'}}={{V}_{C.{C}'{B}'{D}'}}={{V}_{{D}'.DAC}}={{V}_{{B}'.BAC}}=\frac{1}{6}V\).
Vậy \({{V}_{AC{B}'{D}'}}=V-\left( {{V}_{A.{A}'{B}'{D}'}}+{{V}_{C.{C}'{B}'{D}'}}+{{V}_{{D}'.DAC}}+{{V}_{{B}'.BAC}} \right)=V-\frac{4}{6}V=\frac{1}{3}V=\frac{1}{3}.36=12\,\,\left( {{\operatorname{cm}}^{3}} \right)\).
Chọn A
Câu hỏi trước
