Phương pháp giải:

Dựng hình, xác định chiều cao của khối chóp, đưa thể tích về hàm 1 ẩn và khảo sát hàm số tìm max

Lời giải chi tiết:

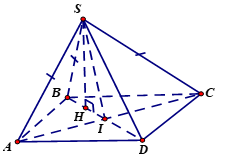
Hình vẽ tham khảo

Gọi \(I\) là tâm hình thoi \(ABCD\), \(H\) là hình chiếu của \(S\) lên mặt phẳng \(\left( ABCD \right)\).

Ta có \(SA=SB=SC\) nên hình chiếu vuông góc của \(S\) xuống mặt phẳng \(\left( ABCD \right)\) trùng với tâm đường tròn ngoại tiếp \(\Delta ABC\) hay \(H\in BI\).

Có \(S{{I}^{2}}=S{{A}^{2}}-I{{A}^{2}}={{a}^{2}}-I{{A}^{2}}\), \(I{{B}^{2}}=A{{B}^{2}}-I{{A}^{2}}={{a}^{2}}-I{{A}^{2}}\) suy ra \(SI=IB\). Khi đó tam giác \(SBD\) vuông tại \(S\). Hoặc \(\Delta ABC=\Delta ASC=\Delta ADC\) \(\left( c-c-c \right)\) nên \(IB=IS=ID\), do đó \(\Delta SBD\) vuông tại \(S\).

Giả sử \(SD=x\). Ta có \(SB.SD=SH.BD\) \(\Leftrightarrow a.x=SH.BD\)\(\Leftrightarrow SH=\frac{a.x}{BD}\)

Ta có \({{V}_{SABCD}}=\frac{1}{3}SH.\frac{1}{2}AC.BD=\frac{1}{3}.\frac{ax}{BD}.\frac{1}{2}AC.BD=\frac{1}{6}ax.AC\)

Lại có \(B{{D}^{2}}=S{{B}^{2}}+S{{D}^{2}}={{a}^{2}}+{{x}^{2}}\) suy ra \(I{{B}^{2}}=\frac{{{a}^{2}}+{{x}^{2}}}{4}\) \(\Rightarrow I{{A}^{2}}={{a}^{2}}-\frac{{{a}^{2}}+{{x}^{2}}}{4}=\frac{3{{a}^{2}}-{{x}^{2}}}{4}\)

Suy ra \(AC=2IA\) \(=2\sqrt{\frac{3{{a}^{2}}-{{x}^{2}}}{4}}\)\(=\sqrt{3{{a}^{2}}-{{x}^{2}}}\)\(\Rightarrow \)\({{V}_{SABCD}}=\frac{1}{6}ax.\sqrt{3{{a}^{2}}-{{x}^{2}}}\le \frac{a}{6}.\frac{{{x}^{2}}+3{{a}^{2}}-{{x}^{2}}}{2}=\frac{{{a}^{3}}}{4}\)

Vậy thể tích lớn nhất của khối chóp \(S.ABCD\) là \(\frac{{{a}^{3}}}{4}\).

Chọn B