Phương pháp giải:

Gắn hệ trục tạ độ hoặc dựng hình xác định góc giữa hai mặt phẳng

Lời giải chi tiết:

Cách 1: Chọn hệ trục tọa độ sao cho \(B\left( 0;0;0 \right)\), \(A\left( a\sqrt{2};0;0 \right)\), \(C\left( 0;a\sqrt{2};0 \right)\), \(S\left( x;y;z \right)\).

Ta có \(\left( ABC \right):z=0\), \(\overrightarrow{AS}=\left( x-a\sqrt{2};y;z \right)\), \(\overrightarrow{CS}=\left( x;y-a\sqrt{2};z \right)\)

Do \(\overrightarrow{AS}.\overrightarrow{AB}=0\)\(\Rightarrow \left( x-a\sqrt{2} \right)a\sqrt{2}=0\)\(\Rightarrow x=a\sqrt{2}\), \(d\left( S,\left( ABC \right) \right)=2a\)\(\Rightarrow z=2a\) \(\left( z>0 \right)\)

Và \(\overrightarrow{CS}.\overrightarrow{CB}=0\)\(\Rightarrow \left( y-a\sqrt{2} \right)a\sqrt{2}=0\)\(\Rightarrow y=a\sqrt{2}\)\(\Rightarrow S\left( a\sqrt{2};a\sqrt{2};2a \right)\).

Lại có \(\overrightarrow{AS}=\left( 0;a\sqrt{2};2a \right)\), \(\overrightarrow{CS}=\left( a\sqrt{2};0;2a \right)\), \(\overrightarrow{BS}=\left( a\sqrt{2};a\sqrt{2};2a \right)\).

Mặt phẳng \(\left( SBC \right)\) có 1 vtpt \(\vec{n}=\left( -\sqrt{2};0;1 \right)\), \(\left( SAB \right)\) có 1 vtpt \(\vec{m}=\left( 0;\sqrt{2};-1 \right)\)\(\Rightarrow \cos \varphi \)\(=\frac{1}{\sqrt{3}.\sqrt{3}}\)\(=\frac{1}{3}\).

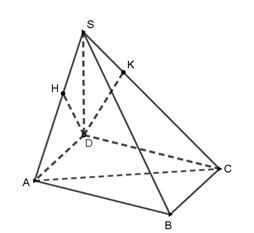
Cách 2: Gọi \(D\) là hình chiếu vuông góc của \(S\) trên mp\(\left( ABC \right)\).

Ta có \(\left. \begin{align} & AB\bot SA \\& AB\bot SD \\\end{align} \right\}\Rightarrow AB\bot AD\), tương tự: \(BC\bot CD\). Vậy \(ABCD\) là hình vuông.

Gọi \(H\), \(K\) lân lượt là hình chiếu của \(D\) trên \(SA\), \(SC\).

Góc giữa hai mặt phẳng \(\left( SAB \right)\) và \(\left( SCB \right)\) là góc giữa hai đường thẳng

\(DH\) và \(DK\).

Tính được \(DH=DK=\frac{2a}{\sqrt{3}}\);  \(\frac{SH}{SA}=\frac{S{{D}^{2}}}{S{{A}^{2}}}=\frac{2}{3}\) \(\Rightarrow HK=\frac{2}{3}AC=\frac{4a}{3}\) .

Tứ đó suy ra \(\cos \widehat{HDK}=\frac{H{{D}^{2}}+K{{D}^{2}}-H{{K}^{2}}}{2HD.KD}=\frac{1}{3}\).

Chọn A