Câu hỏi
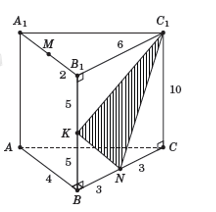
Cho hình lăng trụ đứng \(ABC.{A_1}{B_1}{C_1}\) có đáy \(ABC\) là tam giác vuông tại B, \(AB = 4\), \(BC = 6\), chiều cao của lăng trụ bằng 10. Gọi \(K,\,M,\,N\) lần lượt là trung điểm của các cạnh \(B{B_1},\,\,{A_1}{B_1},\,\,BC\). Thể tích khối tứ diện \({C_1}KMN\) là :
- A \(15\)
- B 5
- C 45
- D 10
Phương pháp giải:
\({V_{{C_1}MNK}} = {V_{M.{C_1}KN}}\)
Lời giải chi tiết:
Ta có \({V_{{C_1}MNK}} = {V_{M.{C_1}KN}}\).
\(\begin{array}{l}M{B_1} \bot \left( {BC{C_1}{B_1}} \right) \Rightarrow {V_{M.{C_1}KN}} = \frac{1}{3}M{B_1}.{S_{{C_1}KN}}\\{S_{{K_1}CN}} = {S_{BC{C_1}{B_1}}} - {S_{K{B_1}{C_1}}} - {S_{NC{C_1}}} - {S_{KBN}}\\\,\,\,\,\,\,\,\,\,\,\,\, = 6.10 - \frac{1}{2}.5.6 - \frac{1}{2}.10.3 - \frac{1}{2}.5.3 = \frac{{45}}{2}\\ \Rightarrow {V_{M.{C_1}KN}} = \frac{1}{3}.2.\frac{{45}}{2} = 15\end{array}\)
Chọn A.
Câu hỏi trước
