Câu hỏi
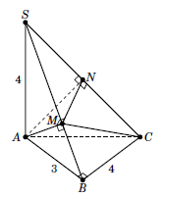
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, \(AB = 3,\,\,BC = 4\), đường thẳng SA vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = 4\). Gọi \(AM,AN\) lần lượt là chiều cao của các tam giác SAB và SAC. Tính thể tích khối tứ diện AMNC ?
- A \(\frac{{128}}{{41}}\)
- B \(\frac{{256}}{{41}}\)
- C \(\frac{{768}}{{41}}\)
- D \(\frac{{384}}{{41}}\)
Phương pháp giải:
Chứng minh \(AM \bot \left( {SBC} \right) \Rightarrow {V_{AMNC}} = \frac{1}{3}AM.{S_{MNC}}\)
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\\\left\{ \begin{array}{l}AM \bot SB\\AM \bot BC\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right) \Rightarrow {V_{AMNC}} = \frac{1}{3}AM.{S_{MNC}}\end{array}\)
\(\left\{ \begin{array}{l}AM \bot SC\\AN \bot SC\end{array} \right. \Rightarrow SC \bot \left( {AMN} \right) \Rightarrow SC \bot MN \Rightarrow \Delta MNC\) vuông tại N.
Ta có \(AM = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{12}}{5};\,\,AN = \frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{20}}{{\sqrt {41} }}\)
\( \Rightarrow MN = \sqrt {A{N^2} - A{M^2}} = \sqrt {\frac{{4096}}{{205}}} = \frac{{64}}{{5\sqrt {41} }}\)
Ta có \(NC = \frac{{A{C^2}}}{{SC}} = \frac{{25}}{{\sqrt {41} }}\).
\( \Rightarrow {V_{AMNC}} = \frac{1}{3}AM.\frac{1}{2}MN.MC = \frac{1}{6}.\frac{{12}}{5}.\frac{{64}}{{5\sqrt {41} }}.\frac{{25}}{{\sqrt {41} }} = \frac{{128}}{{41}}\)
Chọn A.