Câu hỏi
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) cạnh \(2a,\) gọi \(M\) là trung điểm của \(B{B}'\) và \(P\) thuộc cạnh \(D{D}'\) sao cho \(DP\,=\,\frac{1}{4}D{D}'.\) Mặt phẳng \((AMP)\) cắt \(C{C}'\) tại\(N.\) Thể tích khối đa diện \(AMNPBCD\) bằng
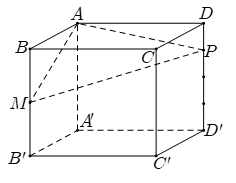
- A \(V=2{{a}^{3}}.\)
- B \(3{{a}^{3}}.\)
- C \(V=\frac{11{{a}^{3}}}{3}.\)
- D \(V=\frac{9{{a}^{3}}}{4}.\)
Phương pháp giải:
Dựa vào công thức tính nhanh tỉ số thể tích trong khối lăng trụ với đáy là tứ giác như sau: Cho hình lăng trụ \(ABCD.{A}'{B}'{C}'{D}'\) với \(M\in A{A}',\,\,N\in B{B}',\,\,P\in C{C}',\,\,Q\in D{D}'\) suy ra
\(\frac{AM}{A{A}'}+\frac{CN}{C{C}'}=\frac{BP}{B{B}'}+\frac{DQ}{D{D}'}\) và \(\frac{{{V}_{ABCD.MNPQ}}}{{{V}_{ABCD.{A}'{B}'{C}'{D}'}}}=\frac{1}{2}\left( \frac{AM}{A{A}'}+\frac{CN}{C{C}'} \right)=\frac{1}{2}\left( \frac{BP}{B{B}'}+\frac{DQ}{D{D}'} \right)\)
Lời giải chi tiết:
Áp dụng công thức tính nhanh, ta có \(\frac{{{V}_{AMNPBCD}}}{{{V}_{ABCD.{A}'{B}'{C}'{D}'}}}=\frac{1}{2}\left( \frac{BM}{B{B}'}+\frac{DP}{D{D}'} \right)=\frac{3}{8}\Rightarrow \,\,{{V}_{AMNPBCD}}=3{{a}^{3}}.\)
Chọn B







