Câu hỏi
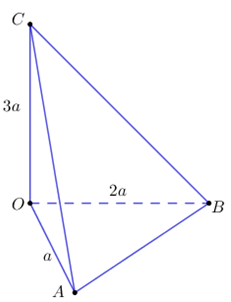
Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau và \(OA\, = \,a,\,\,OB\, = \,2a,\) \(OC\,=\,3a.\) Thể tích của khối tứ diện \(OABC\) bằng
- A \(V=2{{a}^{3}}.\)
- B \(V = \frac{{{a^3}}}{3}.\)
- C \(V=\frac{2{{a}^{3}}}{3}.\)
- D \(V={{a}^{3}}.\)
Phương pháp giải:
Tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) vuông góc với nhau \( \Rightarrow \,\,{V_{O.ABC}} = \frac{{OA.OB.OC}}{6}\)
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OC \bot \left( {OAB} \right) \Rightarrow {V_{OABC}} = \frac{1}{3}.OC.{S_{\Delta \,OAB}} = \frac{{OC.OB.OA}}{6} = {a^3}.\)
Chọn D
Câu hỏi trước
