Câu hỏi
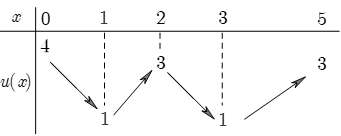
Cho hàm số \(u(x)\) liên tục trên đoạn \(\text{ }\!\![\!\!\text{ }0;\,\,5\text{ }\!\!]\!\!\text{ }\) và có bảng biến thiên như hình vẽ. Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt{3x}+\sqrt{10-2x}=m.u(x)\) có nghiệm trên đoạn \(\text{ }\!\![\!\!\text{ }0;\,\,5\text{ }\!\!]\!\!\text{ }\)?
- A 5
- B 6
- C 3
- D 4
Phương pháp giải:
Cô lập tham số m, khảo sát hàm trên tử số tìm max – min, đánh giá khoảng để phương trình có nghiệm
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy rằng \(v\left( x \right)\in \left[ 1;4 \right]\) với \(\forall x\in \left[ 0;5 \right].\)
Xét hàm số \(f\left( x \right)=\sqrt{3x}+\sqrt{10-2x}\) trên \(\left[ 0;5 \right],\) có \({f}'\left( x \right)=\frac{3}{2\sqrt{3x}}-\frac{1}{\sqrt{10-2x}}=0\Leftrightarrow x=3.\)
Suy ra \(\underset{\left[ 0;5 \right]}{\mathop{\min }}\,f\left( x \right)=f\left( 0 \right)=\sqrt{10};\,\,\underset{\left[ 0;5 \right]}{\mathop{\max }}\,f\left( x \right)=f\left( 3 \right)=5\Rightarrow \,\,\sqrt{10}\le \sqrt{3x}+\sqrt{10-2x}\le 5.\)
Khi đó \(m=\frac{\sqrt{3x}+\sqrt{10-2x}}{u\left( x \right)}\) mà \(\frac{1}{u\left( x \right)}\in \left[ \frac{1}{4};1 \right]\,\,\xrightarrow{{}}\,\,\frac{\sqrt{3x}+\sqrt{10-2x}}{u\left( x \right)}\in \left[ \frac{\sqrt{10}}{4};5 \right].\)
Do đó, phương trình đã cho có nghiệm \(\Leftrightarrow \,\,m\in \left[ \frac{\sqrt{10}}{4};5 \right].\)
Kết hợp \(m\in \mathbb{Z}\,\,\xrightarrow{{}}\) có 5 giá trị nguyên \(m\) cần tìm.
Chọn A