Câu hỏi
Cho các hàm số \(y=f(x)\) và \(y=g(x)\) liên tục trên mỗi khoảng xác định của chúng và có bảng biến thiên được cho như hình vẽ dưới đây.
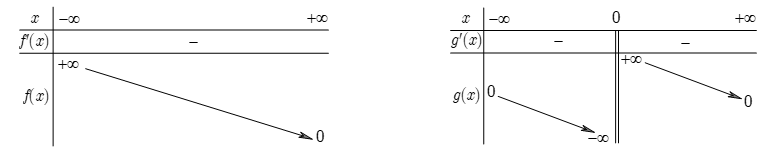
Mệnh đề nào sau đây sai?
- A Phương trình \(f(x)=g(x)\) không có nghiệm thuộc khoảng \((-\infty ;\,\,0).\)
- B Phương trình \(f(x)+g(x)=m\) có nghiệm với mọi \(m.\)
- C Phương trình \(f(x)+g(x)=m\) có \(2\) nghiệm với mọi \(m>0.\)
- D Phương trình \(f(x)=g(x)-1\) không có nghiệm.
Phương pháp giải:
Dựa vào bảng biến thiên để chọn hàm thỏa mãn, sử dụng casio giải quyết các đáp án bài cho
Lời giải chi tiết:
Ta chọn được hàm số \(f\left( x \right)=-\ x+\sqrt{{{x}^{2}}+4}\) thỏa mãn bảng biến thiên.
Thật vậy \({f}'\left( x \right)=-\,1+\frac{x}{\sqrt{{{x}^{2}}+4}}=\frac{x-\sqrt{{{x}^{2}}+4}}{\sqrt{{{x}^{2}}+4}}<0;\text{ }\forall x\in \mathbb{R}.\)
Suy ra \(f\left( x \right)\) là hàm số nghịch biến trên khoảng \(\left( -\,\infty ;+\,\infty \right)\).
Tính \(\underset{x\,\to \,-\,\infty }{\mathop{\lim }}\,f\left( x \right)=+\,\infty \) và \(f\left( x \right)=-\,x+\sqrt{{{x}^{2}}+4}=\frac{1}{x+\sqrt{{{x}^{2}}+4}}\Rightarrow \underset{x\,\,\to \,\,+\,\,\infty }{\mathop{\lim }}\,f\left( x \right)=0.\)
Với \(f\left( x \right)=-\,x+\sqrt{{{x}^{2}}+4}\) và \(g\left( x \right)=\frac{4}{x}\Rightarrow \) Phương trình \(f\left( x \right)=g\left( x \right)-1\) có nghiệm.
Chọn D







