Câu hỏi
Gọi \(\left( C \right)\) là tập hợp các điểm trên mặt phẳng biểu diễn số phức \(z = x - 1 + yi\,\,\left( {x,y \in R} \right)\) thỏa mãn \(\left| z \right| = 1\) và N là điểm biểu diễn cho số phức \({z_0} = 1 - i\). Tìm điểm M thuộc \(\left( C \right)\) sao cho MN có độ dài lớn nhất.
- A
\(M\left( {1;1} \right)\)
- B
\(M\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\)
- C
\(M\left( {1;0} \right)\)
- D \(M\left( {0;0} \right)\)
Phương pháp giải:
+) Tìm phương trình \(\left( C \right)\).
+) Xác định điểm N.
+) Vẽ hình và tìm vị trí của M trên \(\left( C \right)\) để \(M{N_{\max }}\).
Lời giải chi tiết:
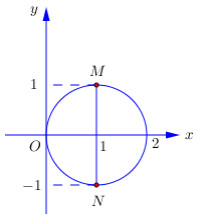
\(\left| z \right| = 1 \Leftrightarrow \left| {x - 1 + yi} \right| = 1 \Leftrightarrow {\left( {x - 1} \right)^2} + {y^2} = 1 \Rightarrow \left( C \right)\)là đường tròn tâm \(I\left( {1;0} \right)\) bán kính \(R = 1\).
Điểm N là điểm biểu diễn cho số phức \({z_0} = 1 - i \Rightarrow N\left( {1; - 1} \right) \Rightarrow N\left( C \right)\).
Dựa vào hình vẽ ta thấy MN lớn nhất \( \Rightarrow MN\) là đường kính của \(\left( C \right) \Rightarrow M\left( {1;1} \right)\).
Chọn A.







