Phương pháp giải:

Khảo sát hàm số đã cho, từ đó đánh giá số giao điểm của đồ thị hàm số với trục hoành.

Lời giải chi tiết:

\(y = {x^4} - {x^3} - 2\)

\(y' = 4{x^3} - 3{x^2} = 0 \Leftrightarrow {x^2}(4x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{3}{4}\end{array} \right.\)

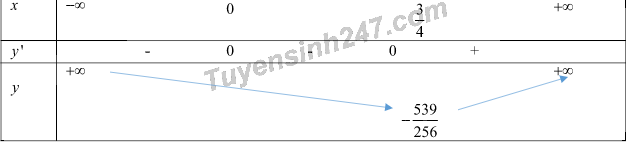
Bảng biến thiên:

Quan sát bảng biến thiên, ta thấy số giao điểm của đồ thị hàm số \(y = {x^4} - {x^3} - 2\) với trục hoành là 2.

Chọn: B