Phương pháp giải:

Đặt \(t = {\cos ^2}x\), sử dụng công thức \(\cos 2x = 2{\cos ^2}x - 1\).

Đưa phương trình về dạng \(f\left( t \right) = m\), lập BBT và biện luận.

Lời giải chi tiết:

\(\begin{array}{l}\,\,\,\,\,4{\cos ^3}2x - 6{\cos ^2}x = m - 4\\ \Leftrightarrow 4{\left( {2{{\cos }^2}x - 1} \right)^3} - 6{\cos ^2}x = m - 4\end{array}\)

Đặt \(t = {\cos ^2}x\,\,\left( {t \in \left[ {0;1} \right]} \right)\), phương trình trở thành: \(4{\left( {2t - 1} \right)^3} - 6t = m - 4\)

\( \Leftrightarrow 32{t^3} - 48{t^2} + 24t - 4 - 6t + 4 = m \Leftrightarrow 32{t^3} - 48{t^2} + 18t = m\)

Xét hàm số \(f\left( t \right) = 32{t^3} - 48{t^2} + 18t\) trên \(\left[ {0;1} \right]\) ta có \(f'\left( t \right) = 96{t^2} - 96t + 18 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \frac{3}{4}\\t = \frac{1}{4}\end{array} \right.\)

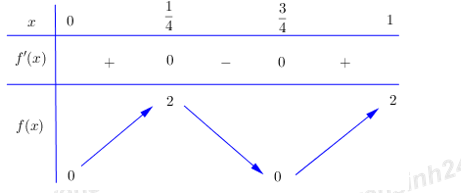
BBT :

Để phương trình có nghiệm \( \Rightarrow m \in \left[ {0;2} \right]\).

Chọn D.