Phương pháp giải:

Đặt \(t = \left| x \right|\,\,\left( {t \ge 0} \right)\).

Lời giải chi tiết:

Đặt \(t = \left| x \right|\,\,\left( {t \ge 0} \right)\), khi đó phương trình trở thành \(\frac{{\left| {t - 2} \right|}}{{t + 1}} = m\,\,\left( 1 \right)\).

Để phương trình ban đầu có 2 nghiệm phân biệt \( \Rightarrow \) phương trình (1) có 1 nghiệm \(t > 0\).

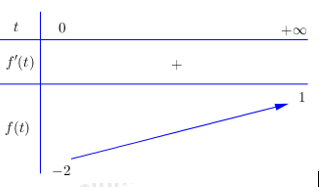
Xét hàm số \(f\left( t \right) = \frac{{t - 2}}{{t + 1}}\,\,\left( {t \ge 0} \right)\) có \(f'\left( t \right) = \frac{3}{{{{\left( {t + 1} \right)}^2}}} > 0\,\,\forall t \ge 0\)

BBT:

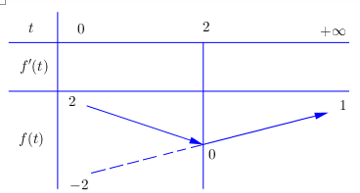
Từ đó ta suy ra BBT của đồ thị hàm số \(g\left( t \right) = \frac{{\left| {t - 2} \right|}}{{t + 1}}\) như sau:

Số nghiệm của phương trình \(\frac{{\left| {t - 2} \right|}}{{t + 1}} = m\) là số giao điểm của đồ thị hàm số \(g\left( t \right) = \frac{{\left| {t - 2} \right|}}{{t + 1}}\) và đường thẳng \(y = m\). Dựa vào BBT ta thấy để phương trình (1) có 1 nghiệm \(t > 0\) thì \(m \in \left[ {1;2} \right] \cup \left\{ 0 \right\}\).

Chọn B.