Câu hỏi
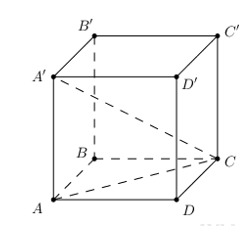
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Tính diện tích xung quanh của hình nón tròn xoay sinh bởi đường gấp khúc ACA’ khi quay quanh trục AA’.
- A \(\pi \sqrt 5 \)
- B \(\pi \sqrt 6 \)
- C \(\pi \sqrt 3 \)
- D \(\pi \sqrt 2 \)
Phương pháp giải:
Diện tích xung quanh của hình nón \({S_{xq}} = \pi rl\) trong đó \(r;l\) lần lượt là bán kính và độ dài đường sinh của hình nón.
Lời giải chi tiết:
Ta có \(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta ACA'\) vuông tại A.
Khi quay tam giác ACA’ quanh cạnh AA’ ta được hình nón có đường cao \(AA' = 1\) và bán kính \(AC = \sqrt 2 \).
Khi đó độ dài đường sinh \(A'C = \sqrt 3 \).
Vậy diện tích xung quang của hình nón là \({S_{xq}} = \pi .AC.A'C = \pi .\sqrt 2 .\sqrt 3 = \pi \sqrt 6 \).
Chọn B.
Câu hỏi trước
