Câu hỏi
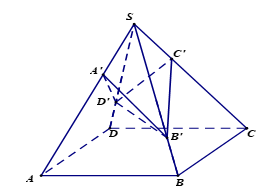
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành và có thể tích \(48\). Trên các cạnh \(SA\),\(SB\),\(SC\),\(SD\) lần lượt lấy các điểm \({A}'\),\({B}'\),\(C'\) và \({D}'\) sao cho \(\frac{S{A}'}{SA}=\frac{S{C}'}{SC}=\frac{1}{3}\) và \(\frac{S{B}'}{SB}=\frac{S{D}'}{SD}=\frac{3}{4}\). Tính thể tích\(V\) của khối đa diện lồi \(S{A}'{B}'{C}'{D}'\).
- A \(V=4\).
- B \(V=6\).
- C \(V = \frac{3}{2}\).
- D \(V=9\).
Phương pháp giải:
Áp dụng công thức tính tỉ số thể số (định lí Simpson)
Lời giải chi tiết:
Ta có
\(V = {V_{SA'B'C'D'}} = {V_{S.D'A'B'}} + {V_{S.D'C'B'}}\)
.
\({{V}_{S.{D}'{A}'{B}'}}=\frac{3}{4}.\frac{1}{3}.\frac{3}{4}.{{V}_{S.DAB}}=\frac{3}{16}.\frac{1}{2}.{{V}_{S.ABCD}}=\frac{3}{32}.48=\frac{9}{2}.\)
Tương tự: \({{V}_{S.{D}'{C}'{B}'}}=\frac{9}{2}\). Vậy \(V=9\).
Chọn D
Câu hỏi trước
