Câu hỏi
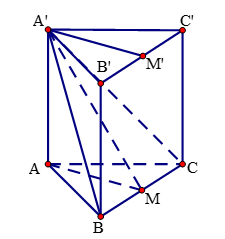
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng . Góc giữa mặt phẳng \(\left( {A}'BC \right)\) và mặt phẳng \(\left( {ABC} \right)\) là . Tính thể tích \(V\) của khối chóp \(A'.BCC'B'.\)
- A
\(V=\frac{{{a}^{3}}\sqrt{3}}{8}\).
- B
\(V = \frac{{3{a^3}\sqrt 3 }}{4}\).
- C
\(V = \frac{{3{a^3}\sqrt 3 }}{8}\).
- D \(V=\frac{{{a}^{3}}\sqrt{3}}{4}\).
Phương pháp giải:
Xác định góc giữa hai mặt phẳng, tính chiều cao và xét tỉ số thể tích khối đa diện
Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(BC\), \(\Delta ABC\) đều nên \(AM\bot BC\)
Mà \(ABC.{A}'{B}'{C}'\) là lăng trụ tam giác đều nên \(\left( ABC \right)\bot \left( {B}'BC{C}' \right)\)
Lại có \(AM\) vuông góc với giao tuyến \(BC\) nên \(AM\bot \left( {B}'BC{C}' \right)\)
\(\Rightarrow {A}'{M}'\bot \left( {B}'BC{C}' \right)\) với \({{V}_{1}}\) là trung điểm của \({B}'{C}'\) \(\Rightarrow {A}'{M}'=d\left( {A}';\left( {B}'BC{C}' \right) \right)\).
Ta có \(\left\{ \begin{align} & AM\bot BC \\& A{A}'\bot BC \\\end{align} \right.\) \(\Leftrightarrow BC\bot \left( A{A}'M \right)\) \(\Leftrightarrow BC\bot {A}'M\)
Lại có \(\left\{ \begin{align} & AM\bot BC;AM\in \left( ABC \right) \\& {A}'M\bot BC;{A}'M\in \left( {A}'BC \right) \\& \left( ABC \right)\cap \left( {A}'BC \right)=BC \\\end{align} \right.\) \(\Leftrightarrow \)\(\measuredangle \left( \left( ABC \right);\left( {A}'BC \right) \right)=\measuredangle \left( AM;{A}'M \right)=\widehat{{A}'MA}=60{}^\circ \)
Ta thấy \(AM\) là đường cao của tam giác đều cạnh \(a\) \(\Rightarrow AM=\frac{a\sqrt{3}}{2}\).
Mặt khác \(\tan \left( \widehat{{A}'MA} \right)=\frac{A{A}'}{AM}\) \(\Leftrightarrow A{A}'=AM\times \tan \left( \widehat{{A}'MA} \right)=\frac{a\sqrt{3}}{2}\tan 60{}^\circ =\frac{3a}{2}=B{B}'=C{C}'\)
Vậy thể tích của khối chóp \({A}'.BC{C}'{B}'\) là
\(V=\frac{1}{3} A’M’ \times S_{BCB’C’} = \frac{1}{3}\frac{a\sqrt{3}}{2} \left(\frac{3a}{2}\times a \right) = \frac{a^3\sqrt{3}}{4}\)
Chọn D