Câu hỏi
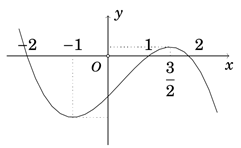
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa \(f\left( 2 \right)=f\left( -2 \right)=0\) và đồ thị hàm số \(y = f'\left( x \right)\) có dạng như hình vẽ bên dưới.
Hàm số \(y = {\left( {f\left( x \right)} \right)^2}\) nghịch biến trên khoảng nào trong các khoảng sau:
- A
\(\left( -1;\frac{3}{2} \right)\).
- B
\(\left( -2;-1 \right)\).
- C
\(\left( -1;1 \right)\).
- D \(\left( 1;2 \right)\).
Phương pháp giải:
Tính đạo hàm của hàm hợp, lập bảng biến thiên xét khoảng nghịch biến
Lời giải chi tiết:
Ta có
Dựa vào đồ thị hàm số\(y = f'\left( x \right)\) ta lập được bảng biến thiên của \(y=f\left( x \right)\) như sau:
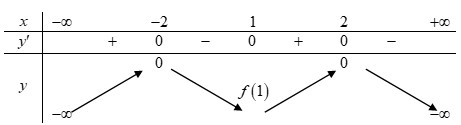
Dựa vào bảng biến thiên ta thấy \(f\left( x \right)\le 0,\,\,\forall x\in \mathbb{R}\).
Xét hàm số \(y = {\left( {f\left( x \right)} \right)^2}\), ta có \({y}'=2f\left( x \right).{f}'\left( x \right)\).
Do \({f}'\left( x \right)>0,\,\,\forall x\in \left( 1;2 \right)\cup \left( -\infty ;-2 \right)\) nên hàm số \(y={{\left( f\left( x \right) \right)}^{2}}\) nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( 1;2 \right)\).
Chọn D