Câu hỏi
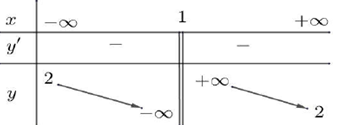
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
- A Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x=1\) và tiệm cận ngang là đường thẳng \(y=2.\)
- B Đồ thị hàm số không có đường tiệm cận.
- C Đồ thị hàm số chỉ có một đường tiệm cận.
- D Đồ thị hàm số có tiệm cận ngang là đường thẳng \(x=1\) và tiệm cận đứng là đường thẳng \(y=2\).
Phương pháp giải:
Dựa vào định nghĩa để xác định đường tiệm cận của đồ thị hàm số
Lời giải chi tiết:
Vì \(\underset{x\ \to \,+\,\infty }{\mathop{\lim }}\,f\left( x \right)=\underset{x\ \to \,-\,\infty }{\mathop{\lim }}\,f\left( x \right)=2\Rightarrow y=2\) là tiệm cận ngang của đồ thị hàm số.
Và \(\underset{x\,\to \,{{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=+\,\infty ;\,\,\underset{x\,\to \,{{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=-\,\infty \Rightarrow \,\,x=1\) là tiệm cận đứng của đồ thị hàm số.
Chọn A