Câu hỏi
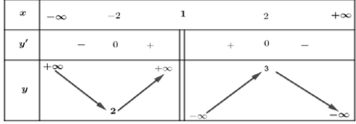
Cho hàm số \(y=f(x)\) liên tục trên \(R\text{ }\!\!\backslash\!\!\text{ }\left\{ 1 \right\}\) và có bảng biến thiên như sau:
Đồ thị hàm số \(y=\frac{1}{2f(x)-5}\) có bao nhiêu đường tiệm cận đứng?
- A 0.
- B 4.
- C 2.
- D 1.
Phương pháp giải:
Định nghĩa tiệm cận đứng của đồ thị hàm số \(y=f(x)\).
Nếu \(\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)=+\infty \,\)hoặc \(\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)=-\infty \,\)hoặc \(\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)=+\infty \,\)hoặc \(\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)=-\infty \,\)thì \(x=a\)
là TCĐ của đồ thị hàm số.
Lời giải chi tiết:
ĐKXĐ của hàm số \(y=\frac{1}{2f(x)-5}=g(x)\) là \(\left\{ \begin{align} x\ne 1 \\ f(x)\ne \frac{5}{2} \\ \end{align} \right.\)
Mà \(f(x)=\frac{5}{2}\) tại 4 điểm phân biệt \({{x}_{1}}<-2<{{x}_{2}}<1<{{x}_{3}}<2<{{x}_{4}}\Rightarrow \)TXĐ: \(D=R\text{ }\!\!\backslash\!\!\text{ }\left\{ 1;{{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\}\)
Ta có:
\(\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,g(x)=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,g(x)=0\)
\(\begin{align} \underset{x\to {{x}_{1}}^{+}}{\mathop{\lim }}\,g(x)=-\infty ,\,\,\underset{x\to {{x}_{1}}^{-}}{\mathop{\lim }}\,g(x)=+\infty \\ \underset{x\to {{x}_{2}}^{+}}{\mathop{\lim }}\,g(x)=+\infty ,\,\,\underset{x\to {{x}_{2}}^{-}}{\mathop{\lim }}\,g(x)=-\infty \\ \underset{x\to {{x}_{3}}^{+}}{\mathop{\lim }}\,g(x)=+\infty ,\,\,\underset{x\to {{x}_{3}}^{-}}{\mathop{\lim }}\,g(x)=-\infty \\ \underset{x\to {{x}_{4}}^{+}}{\mathop{\lim }}\,g(x)=-\infty ,\,\,\underset{x\to {{x}_{4}}^{-}}{\mathop{\lim }}\,g(x)=+\infty \\ \end{align}\)
Vậy, đồ thị hàm số \(y=\frac{1}{2f(x)-5}\) có 4 TCĐ : \(x={{x}_{1}},\,\,x={{x}_{2}},\,\,x={{x}_{3}},\,x={{x}_{4}}\).
Chọn: B