Câu hỏi
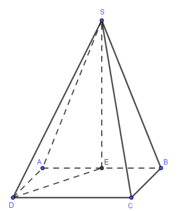
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SD=\frac{3a}{2}\), hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD.
- A \(\frac{{{a}^{3}}}{2}\).
- B \(\frac{{{a}^{3}}}{3}\).
- C \(\frac{{{a}^{3}}}{4}\).
- D \(\frac{2{{a}^{3}}}{3}\).
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp: \(V=\frac{1}{3}S.h\), với S là diện tích của đáy, h là chiều cao của khối chóp.
Lời giải chi tiết:
Gọi E là trung điểm của AB.
Tam giác AED vuông tại A \(\Rightarrow DE=\sqrt{A{{D}^{2}}+A{{E}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{5}}{2}\)
Theo đề bài, ta có : \(SE\bot (ABCD)\).
\(\Rightarrow \Delta SDE\)vuông tại E \(\Rightarrow SE=\sqrt{S{{D}^{2}}-E{{D}^{2}}}=\sqrt{{{\left( \frac{3a}{2} \right)}^{2}}-{{\left( \frac{a\sqrt{5}}{2} \right)}^{2}}}=a\)
Thể tích khối chóp S.ABCD là : \(V=\frac{1}{3}{{S}_{ABCD}}.SE=\frac{1}{3}.{{a}^{2}}.a=\frac{{{a}^{3}}}{3}\).
Chọn: B