Câu hỏi
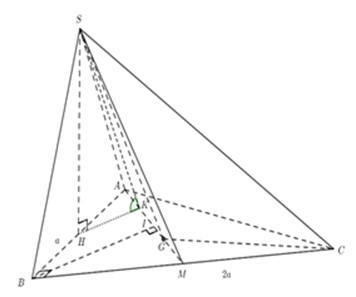
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(B\), \(AB=a;BC=2\text{a}\text{.}\) Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Gọi \(G\) là trọng tâm tam giác \(ABC\), mặt phẳng \(\left( SAG \right)\) tạo với đáy một góc \({{60}^{0}}\). Tính thể tích tứ diện \(ACGS\) bằng
- A \(V=\frac{{{a}^{3}}\sqrt{6}}{36}\cdot \)
- B \(V=\frac{{{a}^{3}}\sqrt{6}}{18}\cdot \)
- C \(V=\frac{{{a}^{3}}\sqrt{3}}{27}\cdot \)
- D \(V=\frac{{{a}^{3}}\sqrt{6}}{12}\cdot \)
Phương pháp giải:
Dựng hình, xác định góc giữa hai mặt phẳng, tính chiều cao và xác định thể tích tứ diện
Lời giải chi tiết:
Gọi \(M\) là trung điểm \(BC\) suy ra \(\Delta ABM\) vuông cân tại \(B\).
Và \(I\) là trung điểm \(AM\Rightarrow AI=\frac{AM}{2}=\frac{\sqrt{A{{B}^{2}}+B{{M}^{2}}}}{2}=\frac{a\sqrt{2}}{2}\cdot \)
Lại có \(K\) là trung điểm \(AI\Rightarrow HK=\frac{BI}{2}=\frac{a\sqrt{2}}{4}\cdot \) Suy ra \(\widehat{\left( SAG \right);\left( ABC \right)}=\widehat{\left( HK;SK \right)}=\widehat{SKH}={{60}^{0}}.\)
Tam giác \(SHK\) vuông tại \(H,\) có \(SH=HK.\tan {{60}^{0}}=\frac{a\sqrt{6}}{4}.\)
Khi đó, thể tích \({{V}_{SABC}}=\frac{1}{3}.\frac{1}{2}.a.2a.\frac{a\sqrt{6}}{4}=\frac{{{a}^{3}}\sqrt{6}}{12}\cdot \)
Dựa vào tam giác ABC vuông tại B và có trọng tâm G.
Ta chứng minh được: \({{S}_{ACG}}=\frac{1}{3}{{S}_{ABC}}.\) \(\Rightarrow {{V}_{S.ACG}}=\frac{1}{3}\cdot {{V}_{S.ABC}}=\frac{{{a}^{3}}\sqrt{6}}{36}\cdot \)
Chọn A