Câu hỏi
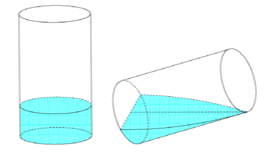
Có một cốc thủy tinh hình trụ, bán kính trong lòng đáy cốc là 6cm, chiều cao trong lòng cốc là 10cm đang đựng một lượng nước. Tính thể tích nước trong cốc, biết khi nghiệm cốc nước vừa lúc khi nước chạm miệng cốc thì ở đáy cốc mực nước trùng với đường kính đáy.
- A \(240c{{m}^{3}}\).
- B \(240\pi c{{m}^{3}}\).
- C \(120c{{m}^{3}}\).
- D \(120\pi c{{m}^{3}}\).
Phương pháp giải:
Ứng dụng tích phân vào tính thể tích.
Lời giải chi tiết:
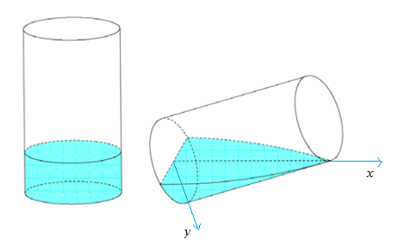
Gắn hệ trục Oxy như hình vẽ.
Nhận xét: Khi cắt phần cốc chứa nước bởi một mặt phẳng vuông góc với Ox , đi qua điểm có hoành độ \(x,\,\,0\le x\le 10\) thì được thiết diện là nửa hình tròn có bán kính là: \(r=\frac{10-x}{10}.R=\frac{6\left( 10-x \right)}{10}\)
Diện tích thiết diện: \(S(x)=\pi {{r}^{2}}=\pi {{\left( \frac{6\left( 10-x \right)}{10} \right)}^{2}}=36\pi .{{\left( 1-\frac{x}{10} \right)}^{2}}=36\pi .\left( 1-\frac{x}{5}+\frac{{{x}^{2}}}{100} \right)\)
Thể tích nước: \(V=\int\limits_{0}^{10}{S(x)dx}=36\pi \int\limits_{0}^{10}{\left( 1-\frac{x}{5}+\frac{{{x}^{2}}}{100} \right)dx}=36\pi \left. \left( x-\frac{{{x}^{2}}}{10}+\frac{{{x}^{3}}}{300} \right) \right|_{0}^{10}=36\pi .\left( 10-10+\frac{1000}{300} \right)=120\pi \left( c{{m}^{3}} \right)\)
Chọn: D