Câu hỏi
Cho hình trụ có bán kính đáy bằng R và chiều cao bằng \(\frac{3R}{2}\). Mặt phẳng \(\left( \alpha \right)\) song song với trục của hình trụ và cách trục một khoảng bằng \(\frac{R}{2}\). Diện tích thiết diện của hình trụ cắt bởi mặt phẳng \(\left( \alpha \right)\) là:
- A
\(\frac{2{{R}^{2}}\sqrt{3}}{3}\)
- B
\(\frac{3{{R}^{2}}\sqrt{3}}{2}\)
- C
\(\frac{3{{R}^{2}}\sqrt{2}}{2}\)
- D \(\frac{2{{R}^{2}}\sqrt{2}}{3}\)
Phương pháp giải:
Mặt phẳng \(\left( \alpha \right)\) song song với trục cắt trụ theo thiết diện là 1 hình chữ nhật.
Lời giải chi tiết:
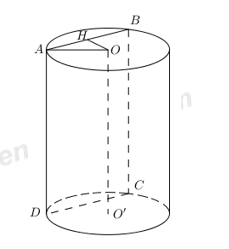
Giả sử \(\left( \alpha \right)\) cắt trụ theo thiết diện là hình chữ nhật ABCD.
Gọi O, O’ lần lượt là tâm hai mặt đáy của hình trụ, H là trung điểm AB ta có \(OH\bot AB\) và \(OH=\frac{R}{2}\) .
\(\begin{align} \Rightarrow AH=\sqrt{A{{O}^{2}}-O{{H}^{2}}}=\frac{R\sqrt{3}}{2}\Rightarrow AB=R\sqrt{3} \\ AD=OO'=\frac{3R}{2} \\ \Rightarrow {{S}_{ABCD}}=AB.AD=R\sqrt{3}.\frac{3R}{2}=\frac{3{{R}^{2}}\sqrt{3}}{2} \\ \end{align}\)
Chọn B.